문제
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
문제 설명
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오.
단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
정점의 개수가 N, 간선의 개수가 M, 시작하는 정점의 번호가 V이다.
다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다.
어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
풀이 방식
나는 문제를 푸는 데 있어서 조금.. 애를 먹었다.그 이유는 그래프에서 DFS와 BFS의 방식을 이해하지 못하고, 자꾸 그래프를 트리처럼 해석하려고 했기 때문이다.
그래서 조금 꼼꼼히 풀이를 적어보려고 한다.
우선 이 문제를 푸는데 있어서 DFS와 BFS 방식을 모르면 안 된다.
만약 잘 모른다면 여기를 참고하도록 하자.
우선 주어진 예제를 가지고 설명을 해 볼 것 이다.
다음 예제는 노드가 4개, 간선이 5개, 시작하는 노드는 1에서 시작한다.
n = 4, m = 5, v = 1
1 2
1 3
1 4
2 4
3 4우선 이 문제는 인접 리스트 또는 인접 행렬 두 방식으로 문제 풀이가 가능하다.
나는 인접 리스트 방식으로 풀었다.

문제에서는 순서가 잘 주어져서 따로 정렬을 할 필요는 없지만, 만약 위 그림의 예제처럼 섞여서 나올 경우 정렬은 필수이다.
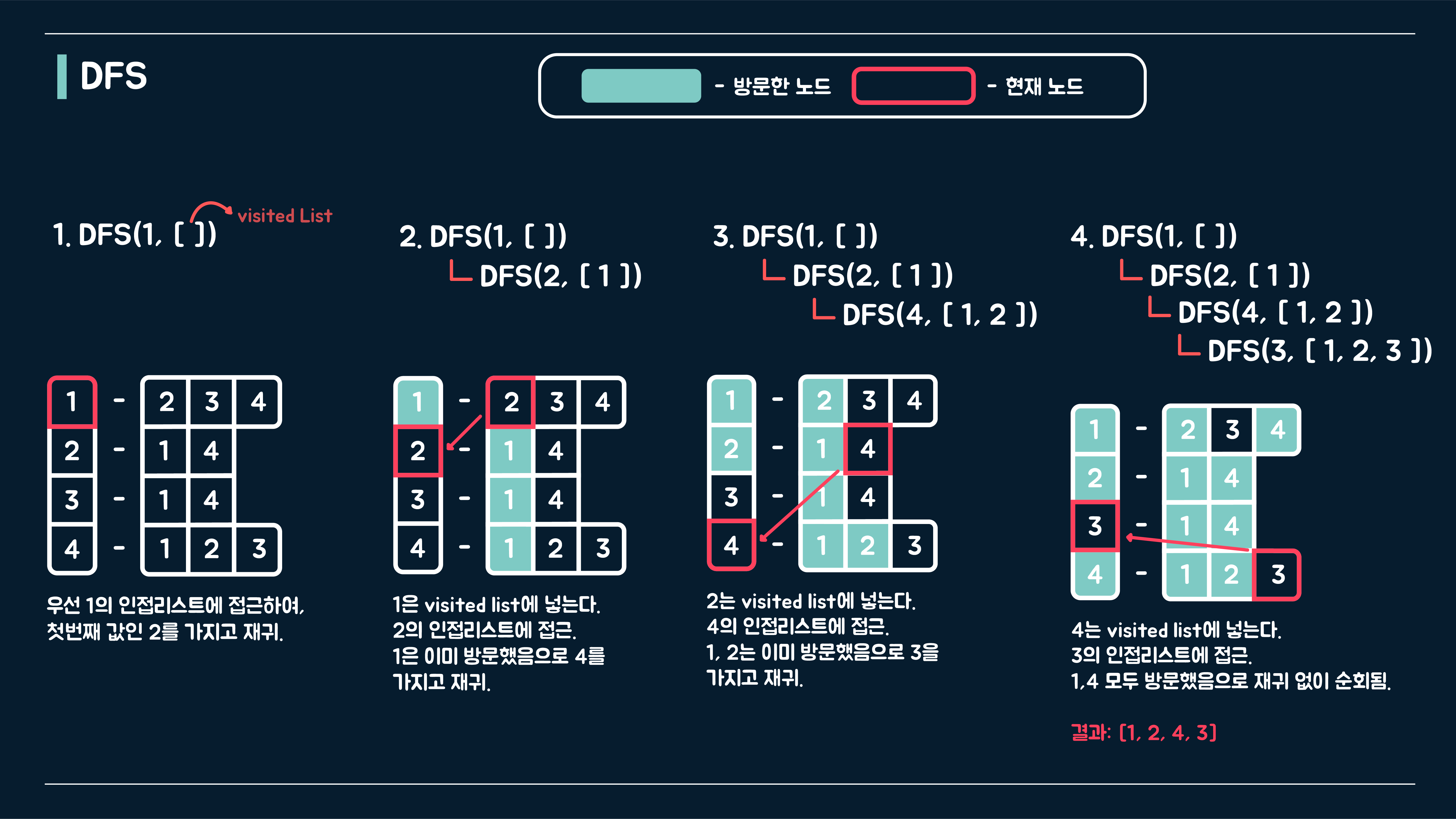
DFS는 재귀 방식으로 풀면 된다. 위 그림을 요약하자면 다음과 같다.
- 현재 노드의 방문 여부를 true로 저장한다.
- 현재 노드에 연결된 다음 노드를 next에 저장
- 만약 방문했다면 그다음 노드로 넘어간다.
- 방문하지 않았다면 DFS()를 다시 실행한다.
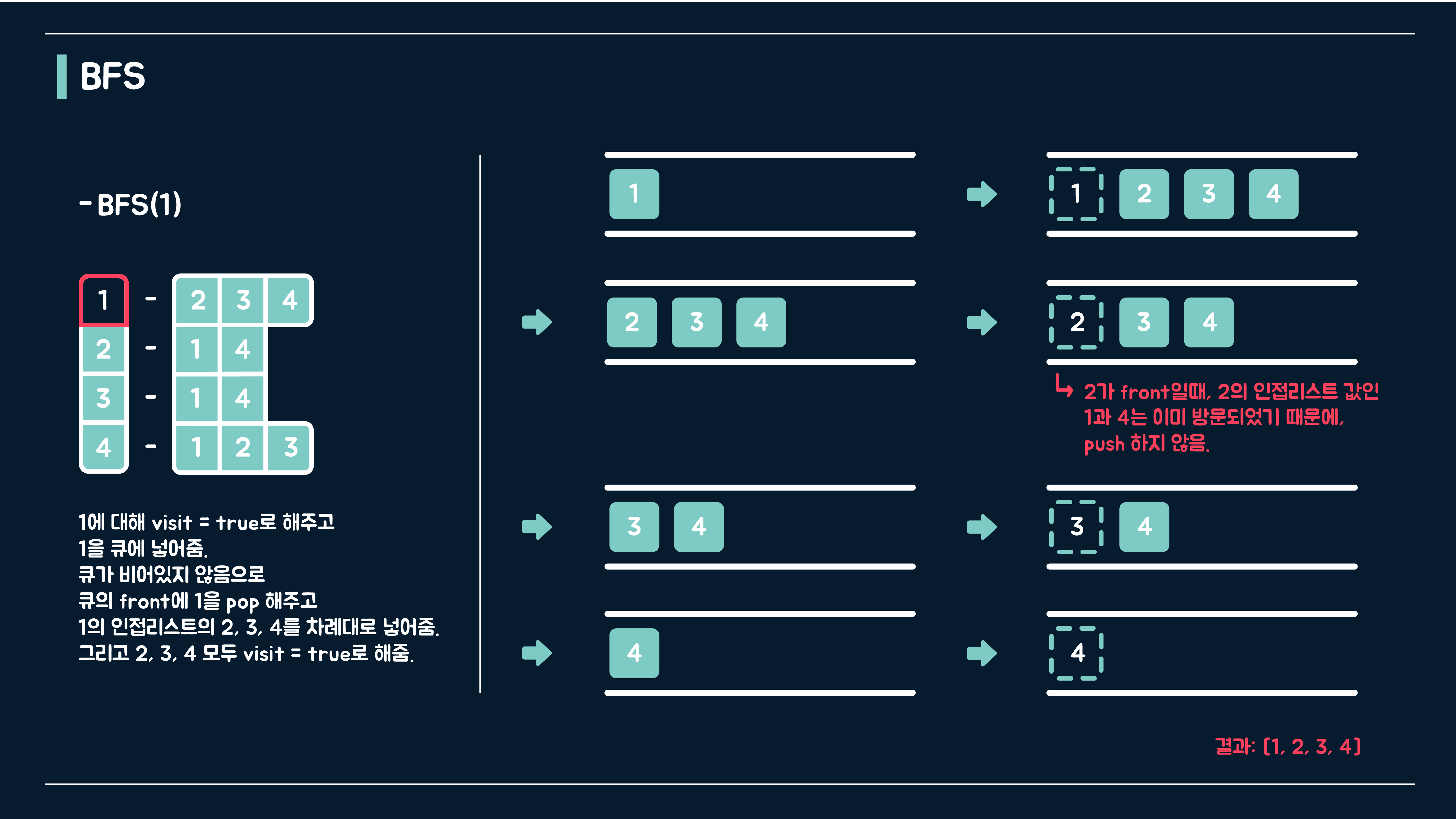
BFS 방식은 Queue 자료구조를 사용하여서 풀면 된다. 위 그림을 요약하자면 다음과 같다.
- 먼저, 각 노드를 방문했는지 체크하는 visit 배열을 초기화한다. (memset 함수)
- BFS()의 입력으로 받은 start 노드를 방문했으니 true로 입력.
- Queue에 start 노드 push 해준다.
만약 Queue가 비어있지 않다면,
- Queue의 가장 앞에 있는 값을 pop 해준다.
- 인접리스트의 원소를 next에 저장한다.
- 인접한 노드 중에서 방문하지 않았다면, true로 바꿔주고 Queue에 push 해준다.
- 인접 리스트 크기만큼 반복한다.
- 위를 계속 반복한다.
솔루션
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m, v;
vector<int> graph[1001];
queue<int> Q;
bool visit[1001];
void BFS(int start)
{
memset(visit, false, sizeof(visit));
Q.push(start);
visit[start] = true;
while (!Q.empty())
{
int now = Q.front();
Q.pop();
cout << now << " ";
for (int i = 0; i < graph[now].size(); i++)
{
int next = graph[now][i];
if (!visit[next])
{
Q.push(next);
visit[next] = true;
}
}
}
}
void DFS(int start)
{
visit[start] = true;
cout << start << " ";
for (int i = 0; i < graph[start].size(); i++)
{
int next = graph[start][i];
if (!visit[next])
DFS(next);
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m >> v;
while (m--)
{
int x, y;
cin >> x >> y;
graph[x].push_back(y);
graph[y].push_back(x);
}
for (int i = 1; i <= n; i++)
{
sort(graph[i].begin(), graph[i].end());
// 인접리스트 정렬
}
DFS(v);
cout << "\n";
BFS(v);
}여담
이게 왜 실버 2인지 잘 모르겠다.. 체감상 골드 5 정도는 될 거 같은데 어떻게 보면 기초적인 부분이기는 하지만 이해하는 것과 구현하는 것에 난이도 차이가 있는 건 확실한 것 같다.
사실 이 문제를 예전에 풀었다가 너무 어려워서 한동안 도망치고 안 풀었었다.
하지만 다른 문제를 풀기 위해서는 꼭 정복해야 하는 부분이긴 하다.
앞으로는 못하는 게 있다면 피하지 말고 시간이 걸리더라도 부딪히는 자세를 익혀야겠다.
'알고리즘 > 백준' 카테고리의 다른 글
| [C++ / 2751] 수 정렬하기 2 (0) | 2023.08.13 |
|---|---|
| [C++ / 9095] 1, 2, 3 더하기 (0) | 2023.08.08 |
| [C++ / 2293] 동전 1 (0) | 2023.08.03 |
| [C++ / 11053] 가장 긴 증가하는 부분 수열 (0) | 2023.07.30 |
| [C++ / 2012] 등수 매기기 (0) | 2023.07.29 |