728x90
인접 행렬 (Adjacency Matrix)
두 정점 간의 연결 관계를 N x N 크기의 행렬(2차원 배열)로 나타냄.


- 특정 노드와 연결되어 있는 모든 노드 확인: O(N)
- 두 정점 간의 연결 관계 확인: O(1)
- 공간 복잡도: O(N^2)
- 정점이 많아지면 메모리 초과로 인해 사용 불가
- 무방향 그래프의 경우, 주대각선을 기준으로 대칭인 성질을 지닌다.
인접 행렬의 장점 & 단점
[ 장점 ]
- 구현이 쉬움.
- 두 정점간의 연결 관계 확인해야 하는 경우, 확인이 쉽다.
[ 단점 ]
- 특정 노드와 연결된 모든 노드를 검색해야 할 경우, 노드 개수 O(N) 만큼의 시간복잡도를 지님.
- 전체 노드 탐색 시 시간복잡도: O(N^2)
인접 행렬 구현
//해당 인접 행렬은 무방향 그래프의 경우이다.
#include <iostream>
using namespace std;
int main() {
int n, m;
int adj[10][10];
cin >> n >> m;
for (int i=0; i<m; i++) {
int a, b;
cin >> a >> b;
adj[a][b] = 1;
adj[b][a] = 1;
}
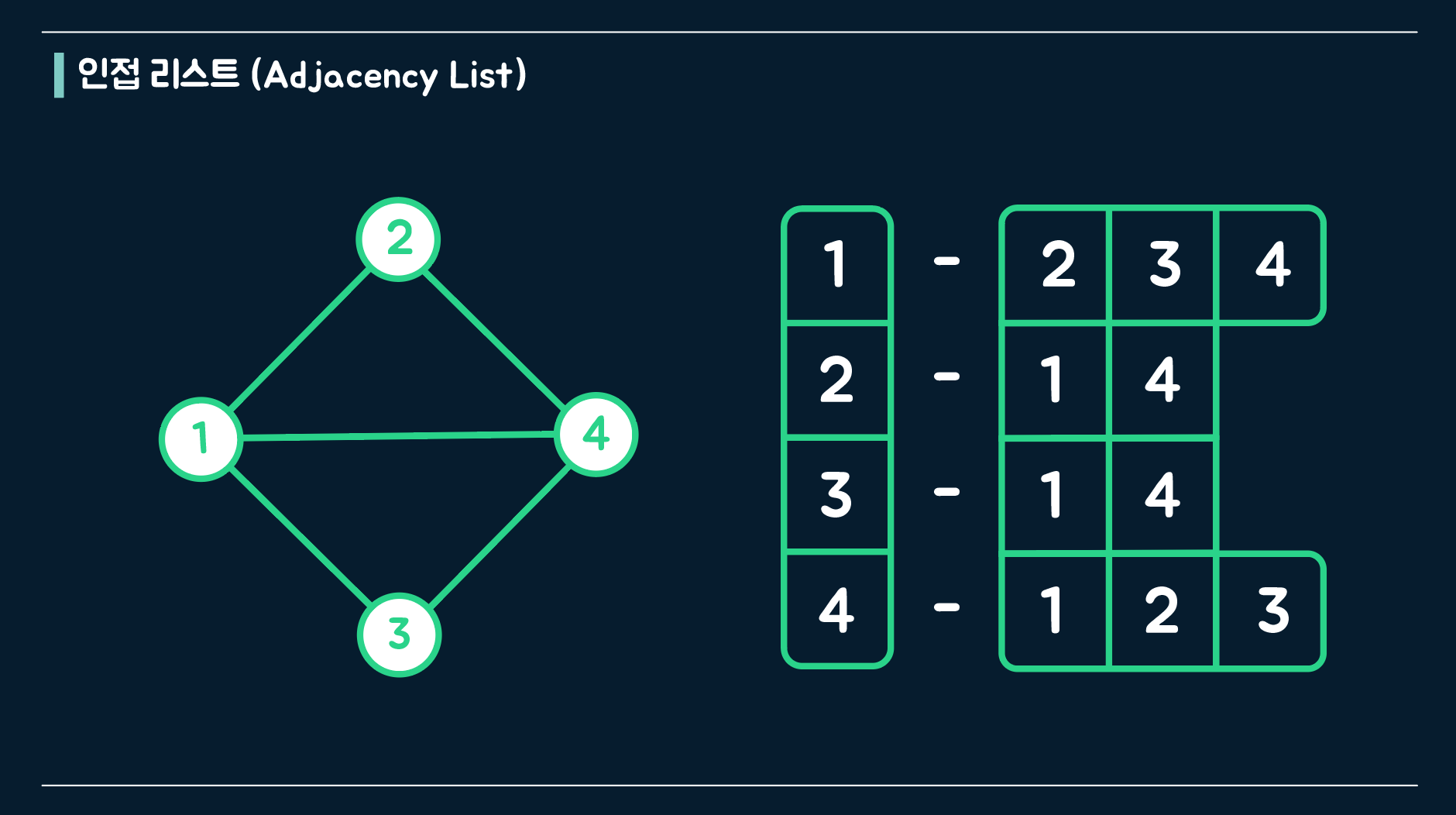
}인접 리스트 (Adjacency List)
각 정점에 연결된 정점들을 리스트(1차원 배열)에 담아 보관함.

- 두 정점간의 연결 관계 확인: O(min(degree(i), degree(j)))
- 특정 노드와 연결되어 있는 모든 노드 확인: O(degree(i))
- 공간 복잡도: O(N+Edge)
인접 리스트의 장점 & 단점
[ 장점 ]
- 실제로 연결된 노드만 저장.
- 모든 vector의 원소의 개수 합 = 간선의 개수
- 정점 사이의 간선이 적은 경우 좋음.
- 연결된 정점들을 탐색해야 하는 경우 사용.
[ 단점 ]
- 단지 노드가 서로 연결되어 있는지 확인하는데 오래걸림.
- 인접 행렬은 adj[i][j] = 1인지 확인만 하면 되지만, 인접리스트의 경우 adj[i]가 j를 원소로 가지는 지 확인해봐야 하기 때문.
인접 리스트 구현
// 해당 인접 리스트는 무방향 그래프의 경우이다.
#include <iostream>
using namespace std;
int main() {
int n, m;
vector<int> adj[10];
cin >> n >> m;
for (int i=0; i<n; i++) {
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
}요약
[ 인접 행렬 ]
- 정점 사이의 연결 관계(간선)가 많을 경우.
- 특정 정점과 정점의 연결 관계를 많이 확인해야 하는 경우. (adj[i][j] = 1 체크)
[ 인접 리스트 ]
- 정점 사이의 연결관계(간선)가 적은 경우.
- 연결된 정점들을 탐색해야 하는 경우. (현재 노드의 인접 리스트에 접근하여, 다음 노드를 탐색)
'Algorism(PS) > 알고리즘 정리' 카테고리의 다른 글
| 분할 정복 (Devide & Conquer) (0) | 2023.07.22 |
|---|---|
| 그리디 알고리즘 (Greedy Algorithm) (0) | 2023.07.20 |
| 다이나믹 프로그래밍(Dynamic Programming) (26) | 2023.07.19 |
| 백트래킹(Back Tracking) (0) | 2023.07.17 |
